Review of Propositional Logic, Part 2

Semantics

In this post we look at the semantics of propositional logic. We begin by discussing truth tables.

Truth tables and equivalence

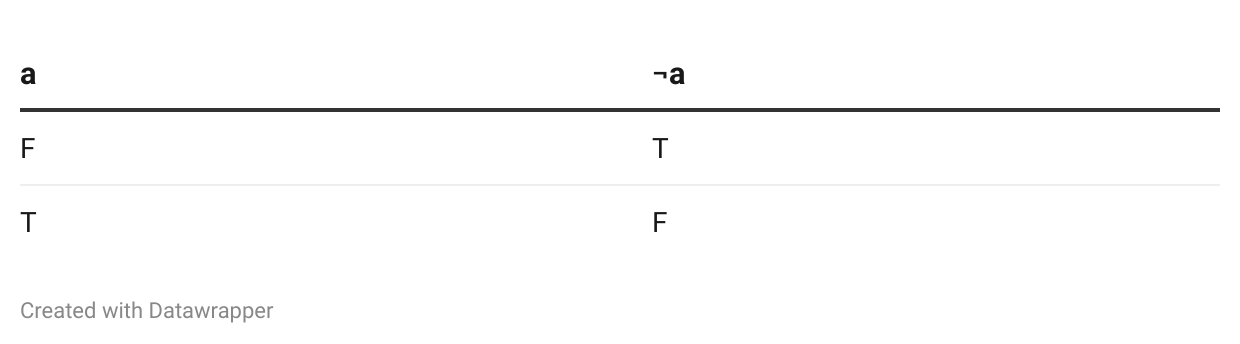
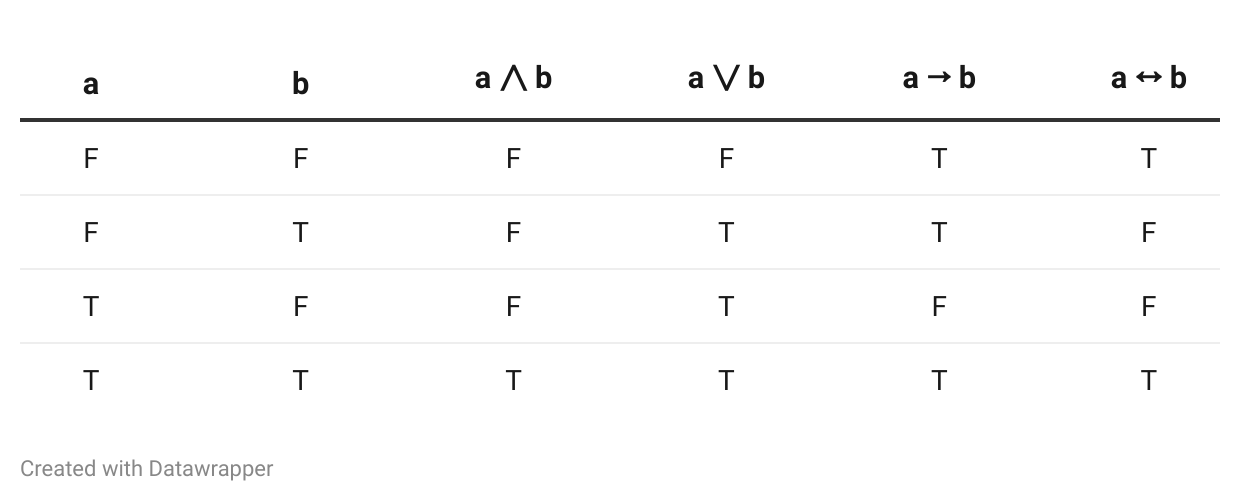
A truth table lists the truth value of a compound proposition for all possible combinations of truth values of the propositions from which it was constructed. Here are the truth tables for the various logical operators, writing “F” for “false” and “T” for “true”:

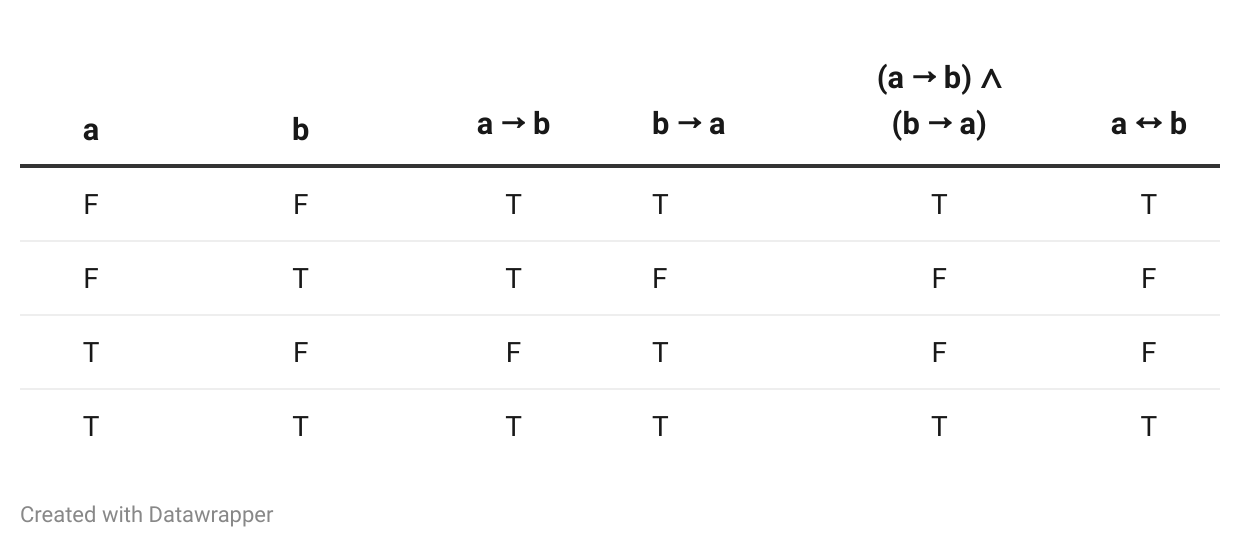
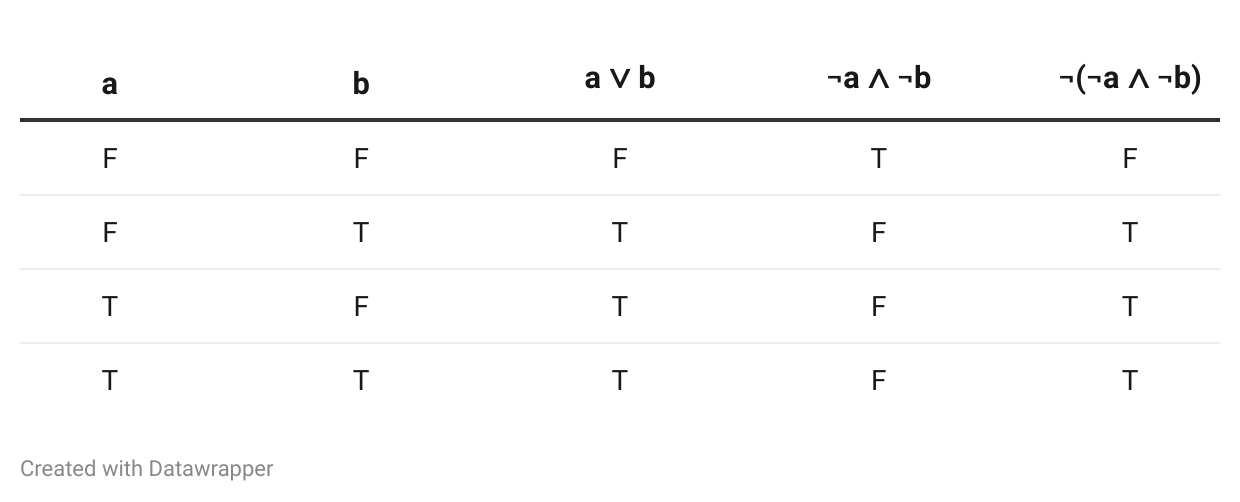
We can use truth tables to show that two propositional formulas are equivalent, that is, have the same truth value regardless of what combination of truth values we assign to the atomic propositions. Here are three important examples:

• a → b is equivalent to ¬a ∨ b.

  

• a ↔︎ b is equivalent to (a → b) ∧ (b → a).

  

• a ∨ b is equivalent to ¬(¬a ∧ ¬b).

  

From these equivalences we can see that we really only need the logical operators NOT (¬) and AND (∧), since all the others can be defined in terms of them.

Truth assignments

In mathematical logic an interpretation assigns some sort of value to each of the symbols used (aside from logical operators), and this can then be used to evaluate the truth value of a logical formula. In the specific case of propositional logic, an interpretation is a truth assignment: a function that assigns a value of true or false to each member of a set of propositional symbols. (In predicate logic an interpretation assigns values to constant symbols, variables, and function symbols.)

In the truth tables we saw for the binary logical operators, each row corresponds to one of these four truth assignments:

\(\begin{gather*} \{ \mathtt{a} \mapsto F, \mathtt{b} \mapsto F \}, \\ \{ \mathtt{a} \mapsto F, \mathtt{b} \mapsto T \}, \\ \{ \mathtt{a} \mapsto T, \mathtt{b} \mapsto F \}, \\ \{ \mathtt{a} \mapsto T, \mathtt{b} \mapsto T \} \end{gather*}\)

A truth assignment on a particular set of symbols is one that assigns a truth value for each of the symbols in that set. Thus the four truth assignments shown above are all truth assignments on the set { a, b }. It’s also possible to have a truth assignment on an infinite set such as our set Σ of all propositional symbols.

A truth assignment on a propositional formula A is a truth assignment on the propositional symbols appearing in A. For example, the four truth assignments shown above are truth assignments on ¬(¬a ∧ ¬b) but not on (a ∧ b) ∨ ¬c.

Evaluating propositional formulas

Given a propositional formula A and a truth assignment α on the propositional symbols it contains, we write α⟦A⟧ for the results of substituting in the assigned values for the propositional symbols and then evaluating each of the logical operations. For example, if

\(\alpha = \{ \mathtt{a} \mapsto F, \mathtt{b} \mapsto T \}\)

then

\(\begin{eqnarray*} \alpha[[\mathtt{a} \lor \neg\mathtt{b}]] &=& F \lor \neg T \\ &=& F \lor F \\ &=& F \end{eqnarray*}\)

Strictly speaking, we are using ⋁ and ¬ in two different ways above. Within the Oxford brackets ⟦ ⟧, ⋁ and ¬ are merely textual symbols; outside of these brackets they are the actual logical operations.

Satisfaction, contradictions, and tautologies

A truth assignment α on a propositional formula A is said to satisfy the formula A if α⟦A⟧ = T. For example,

\(\{ \mathtt{a} \mapsto F, \mathtt{b} \mapsto T \} \mbox{ satisfies } (\mathtt{a} \rightarrow \mathtt{b}) \wedge \mathtt{b}\)

and

\(\{ \mathtt{a} \mapsto T, \mathtt{b} \mapsto F, \mathtt{c} \mapsto F \} \mbox{ does not satisfy } \mathtt{c} \lor (\mathtt{a} \leftrightarrow \mathtt{b}).\)

A propositional formula is satisfiable if there exists at least one truth assignment that satisfies it. For example,

\((\mathtt{a} \rightarrow \mathtt{b}) \wedge \mathtt{b} \mbox{ is satisfiable }\)

but

\(\mathtt{a} \wedge \neg\mathtt{a} \mbox{ is not satisfiable }.\)

An unsatisfiable propositional formula is also called a contradiction. You don’t even have to know what its propositional symbols mean to know that a contradiction is false.

A propositional formula A is logically valid if every truth assignment on A satisfies A. A logically valid formula is also called a tautology. You don’t even have to know what its propositional symbols mean to know that a tautology is true.

Our definition of a propositional formula doesn’t include any constants for false and true. We don’t strictly need them, as we can use any contradiction for “false” and any tautology for “true.” So as a notational convention, within a propositional formula,

• F means “insert some contradiction here,” and

• T means “insert some tautology here.”